On this put up, I’ll introduce a reinforcement studying (RL) algorithm based mostly on an “various” paradigm: divide and conquer. In contrast to conventional strategies, this algorithm is not based mostly on temporal distinction (TD) studying (which has scalability challenges), and scales effectively to long-horizon duties.
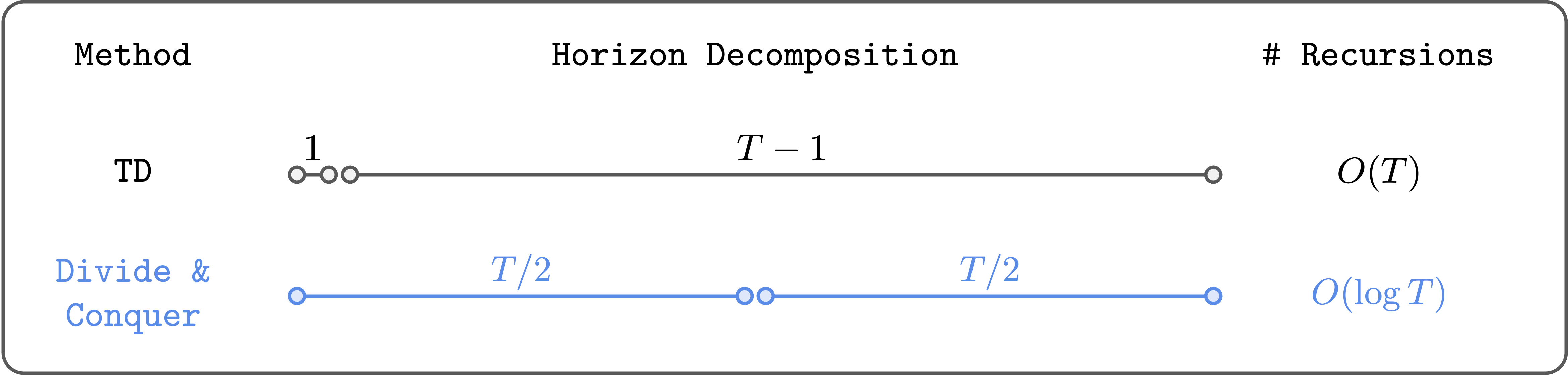
We are able to do Reinforcement Studying (RL) based mostly on divide and conquer, as a substitute of temporal distinction (TD) studying.
Downside setting: off-policy RL
Our drawback setting is off-policy RL. Let’s briefly evaluation what this implies.
There are two lessons of algorithms in RL: on-policy RL and off-policy RL. On-policy RL means we will solely use contemporary information collected by the present coverage. In different phrases, we’ve got to throw away outdated information every time we replace the coverage. Algorithms like PPO and GRPO (and coverage gradient strategies usually) belong to this class.
Off-policy RL means we don’t have this restriction: we will use any sort of information, together with outdated expertise, human demonstrations, Web information, and so forth. So off-policy RL is extra common and versatile than on-policy RL (and naturally tougher!). Q-learning is probably the most well-known off-policy RL algorithm. In domains the place information assortment is pricey (e.g., robotics, dialogue techniques, healthcare, and many others.), we frequently haven’t any alternative however to make use of off-policy RL. That’s why it’s such an essential drawback.
As of 2025, I feel we’ve got fairly good recipes for scaling up on-policy RL (e.g., PPO, GRPO, and their variants). Nonetheless, we nonetheless haven’t discovered a “scalable” off-policy RL algorithm that scales effectively to complicated, long-horizon duties. Let me briefly clarify why.
Two paradigms in worth studying: Temporal Distinction (TD) and Monte Carlo (MC)
In off-policy RL, we sometimes practice a worth perform utilizing temporal distinction (TD) studying (i.e., Q-learning), with the next Bellman replace rule:
[begin{aligned} Q(s, a) gets r + gamma max_{a’} Q(s’, a’), end{aligned}]
The issue is that this: the error within the subsequent worth $Q(s’, a’)$ propagates to the present worth $Q(s, a)$ by way of bootstrapping, and these errors accumulate over your complete horizon. That is mainly what makes TD studying wrestle to scale to long-horizon duties (see this put up for those who’re excited about extra particulars).
To mitigate this drawback, folks have blended TD studying with Monte Carlo (MC) returns. For instance, we will do $n$-step TD studying (TD-$n$):
[begin{aligned} Q(s_t, a_t) gets sum_{i=0}^{n-1} gamma^i r_{t+i} + gamma^n max_{a’} Q(s_{t+n}, a’). end{aligned}]
Right here, we use the precise Monte Carlo return (from the dataset) for the primary $n$ steps, after which use the bootstrapped worth for the remainder of the horizon. This fashion, we will cut back the variety of Bellman recursions by $n$ occasions, so errors accumulate much less. Within the excessive case of $n = infty$, we get better pure Monte Carlo worth studying.
Whereas it is a affordable answer (and sometimes works effectively), it’s extremely unsatisfactory. First, it doesn’t essentially resolve the error accumulation drawback; it solely reduces the variety of Bellman recursions by a continuing issue ($n$). Second, as $n$ grows, we undergo from excessive variance and suboptimality. So we will’t simply set $n$ to a big worth, and have to rigorously tune it for every job.
Is there a essentially totally different option to resolve this drawback?
The “Third” Paradigm: Divide and Conquer
My declare is {that a} third paradigm in worth studying, divide and conquer, might present a perfect answer to off-policy RL that scales to arbitrarily long-horizon duties.
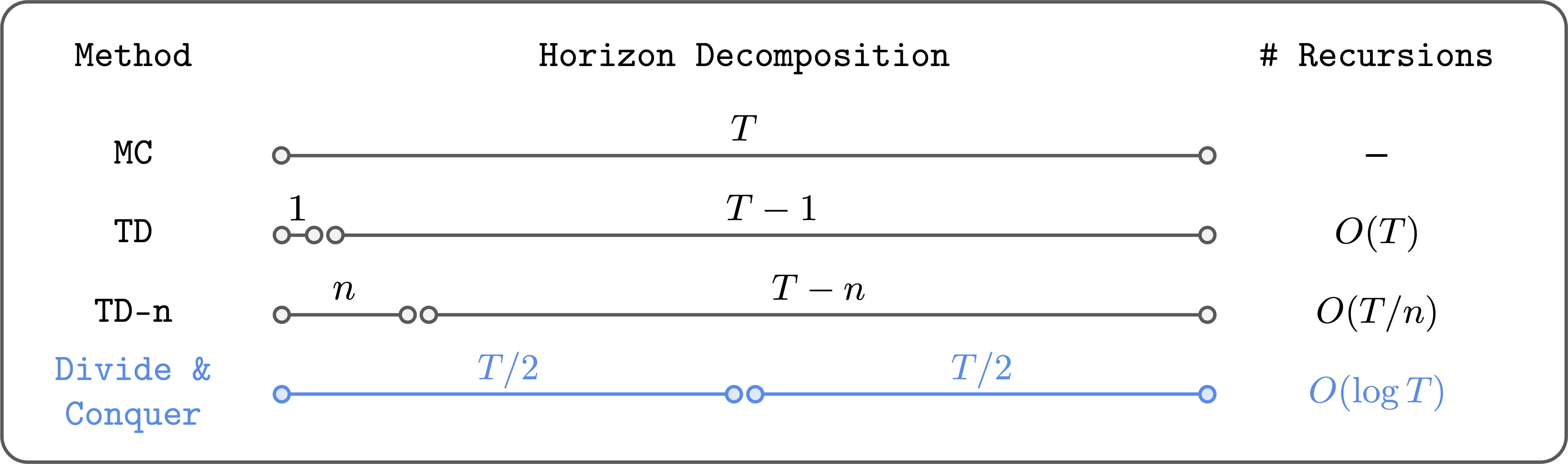
Divide and conquer reduces the variety of Bellman recursions logarithmically.
The important thing concept of divide and conquer is to divide a trajectory into two equal-length segments, and mix their values to replace the worth of the complete trajectory. This fashion, we will (in principle) cut back the variety of Bellman recursions logarithmically (not linearly!). Furthermore, it doesn’t require selecting a hyperparameter like $n$, and it doesn’t essentially undergo from excessive variance or suboptimality, not like $n$-step TD studying.
Conceptually, divide and conquer actually has all the great properties we would like in worth studying. So I’ve lengthy been enthusiastic about this high-level concept. The issue was that it wasn’t clear tips on how to truly do that in apply… till not too long ago.
A sensible algorithm
In a current work co-led with Aditya, we made significant progress towards realizing and scaling up this concept. Particularly, we had been in a position to scale up divide-and-conquer worth studying to extremely complicated duties (so far as I do know, that is the primary such work!) at the very least in a single essential class of RL issues, goal-conditioned RL. Purpose-conditioned RL goals to study a coverage that may attain any state from another state. This supplies a pure divide-and-conquer construction. Let me clarify this.
The construction is as follows. Let’s first assume that the dynamics is deterministic, and denote the shortest path distance (“temporal distance”) between two states $s$ and $g$ as $d^*(s, g)$. Then, it satisfies the triangle inequality:
[begin{aligned} d^*(s, g) leq d^*(s, w) + d^*(w, g) end{aligned}]
for all $s, g, w in mathcal{S}$.
When it comes to values, we will equivalently translate this triangle inequality to the next “transitive” Bellman replace rule:
[begin{aligned}
V(s, g) gets begin{cases}
gamma^0 & text{if } s = g, \
gamma^1 & text{if } (s, g) in mathcal{E}, \
max_{w in mathcal{S}} V(s, w)V(w, g) & text{otherwise}
end{cases}
end{aligned}]
the place $mathcal{E}$ is the set of edges within the atmosphere’s transition graph, and $V$ is the worth perform related to the sparse reward $r(s, g) = 1(s = g)$. Intuitively, which means that we will replace the worth of $V(s, g)$ utilizing two “smaller” values: $V(s, w)$ and $V(w, g)$, supplied that $w$ is the optimum “midpoint” (subgoal) on the shortest path. That is precisely the divide-and-conquer worth replace rule that we had been searching for!
The issue
Nonetheless, there’s one drawback right here. The problem is that it’s unclear how to decide on the optimum subgoal $w$ in apply. In tabular settings, we will merely enumerate all states to search out the optimum $w$ (that is basically the Floyd-Warshall shortest path algorithm). However in steady environments with giant state areas, we will’t do that. Principally, for this reason earlier works have struggled to scale up divide-and-conquer worth studying, despite the fact that this concept has been round for many years (in actual fact, it dates again to the very first work in goal-conditioned RL by Kaelbling (1993) – see our paper for an extra dialogue of associated works). The principle contribution of our work is a sensible answer to this concern.
The answer
Right here’s our key concept: we limit the search house of $w$ to the states that seem within the dataset, particularly, people who lie between $s$ and $g$ within the dataset trajectory. Additionally, as a substitute of trying to find the optimum $textual content{argmax}_w$, we compute a “gentle” $textual content{argmax}$ utilizing expectile regression. Specifically, we decrease the next loss:
[begin{aligned} mathbb{E}left[ell^2_kappa (V(s_i, s_j) – bar{V}(s_i, s_k) bar{V}(s_k, s_j))right], finish{aligned}]
the place $bar{V}$ is the goal worth community, $ell^2_kappa$ is the expectile loss with an expectile $kappa$, and the expectation is taken over all $(s_i, s_k, s_j)$ tuples with $i leq okay leq j$ in a randomly sampled dataset trajectory.
This has two advantages. First, we don’t want to look over your complete state house. Second, we stop worth overestimation from the $max$ operator by as a substitute utilizing the “softer” expectile regression. We name this algorithm Transitive RL (TRL). Try our paper for extra particulars and additional discussions!
Does it work effectively?
humanoidmaze
puzzle
To see whether or not our technique scales effectively to complicated duties, we straight evaluated TRL on among the most difficult duties in OGBench, a benchmark for offline goal-conditioned RL. We primarily used the toughest variations of humanoidmaze and puzzle duties with giant, 1B-sized datasets. These duties are extremely difficult: they require performing combinatorially complicated expertise throughout as much as 3,000 atmosphere steps.
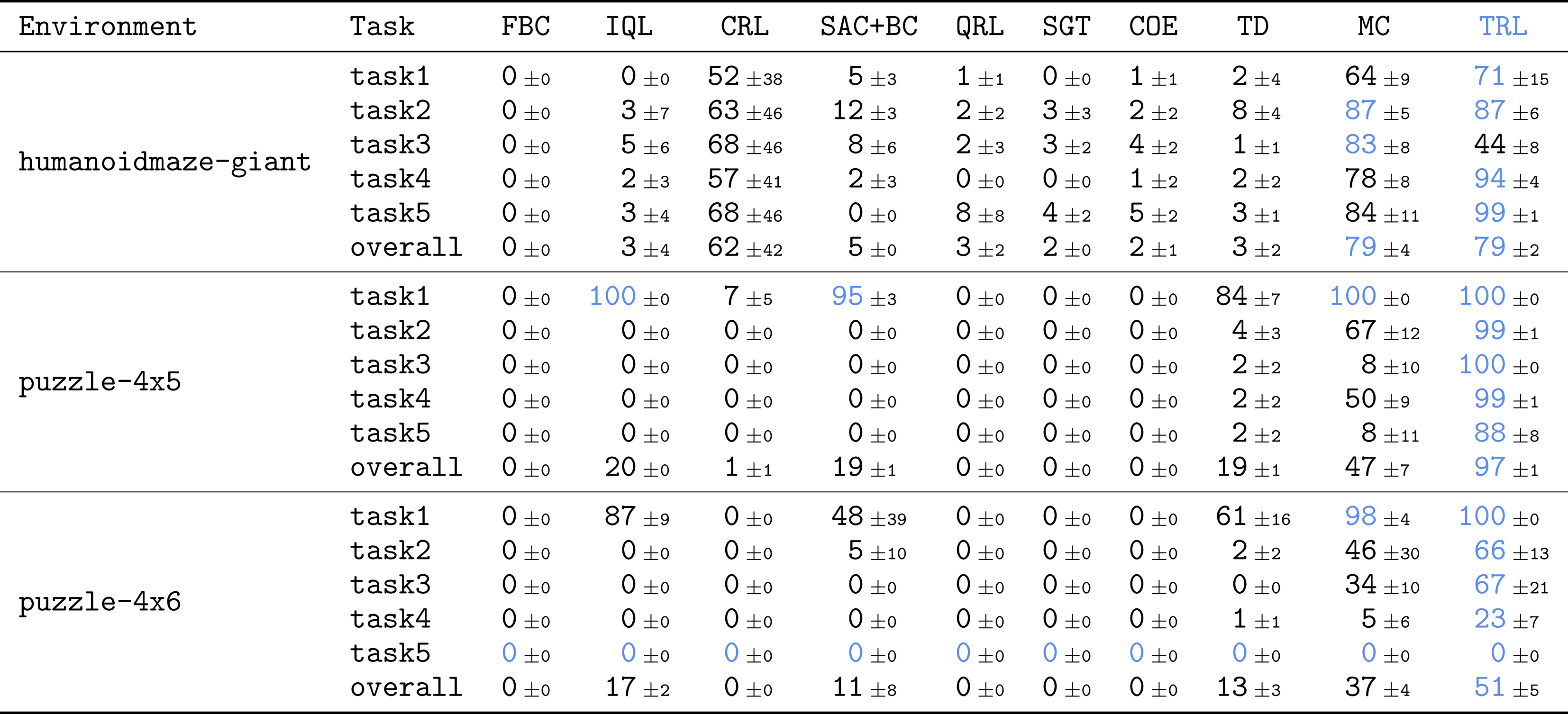
TRL achieves the most effective efficiency on extremely difficult, long-horizon duties.
The outcomes are fairly thrilling! In comparison with many robust baselines throughout totally different classes (TD, MC, quasimetric studying, and many others.), TRL achieves the most effective efficiency on most duties.
TRL matches the most effective, individually tuned TD-$n$, while not having to set $boldsymbol{n}$.
That is my favourite plot. We in contrast TRL with $n$-step TD studying with totally different values of $n$, from $1$ (pure TD) to $infty$ (pure MC). The result’s very nice. TRL matches the most effective TD-$n$ on all duties, while not having to set $boldsymbol{n}$! That is precisely what we needed from the divide-and-conquer paradigm. By recursively splitting a trajectory into smaller ones, it could possibly naturally deal with lengthy horizons, with out having to arbitrarily select the size of trajectory chunks.
The paper has quite a lot of further experiments, analyses, and ablations. For those who’re , take a look at our paper!
What’s subsequent?
On this put up, I shared some promising outcomes from our new divide-and-conquer worth studying algorithm, Transitive RL. That is just the start of the journey. There are lots of open questions and thrilling instructions to discover:
-
Maybe a very powerful query is tips on how to prolong TRL to common, reward-based RL duties past goal-conditioned RL. Would common RL have an identical divide-and-conquer construction that we will exploit? I’m fairly optimistic about this, provided that it’s attainable to transform any reward-based RL job to a goal-conditioned one at the very least in principle (see web page 40 of this e-book).
-
One other essential problem is to take care of stochastic environments. The present model of TRL assumes deterministic dynamics, however many real-world environments are stochastic, primarily on account of partial observability. For this, “stochastic” triangle inequalities would possibly present some hints.
-
Virtually, I feel there may be nonetheless quite a lot of room to additional enhance TRL. For instance, we will discover higher methods to decide on subgoal candidates (past those from the identical trajectory), additional cut back hyperparameters, additional stabilize coaching, and simplify the algorithm much more.
Generally, I’m actually excited in regards to the potential of the divide-and-conquer paradigm. I nonetheless suppose some of the essential issues in RL (and even in machine studying) is to discover a scalable off-policy RL algorithm. I don’t know what the ultimate answer will seem like, however I do suppose divide and conquer, or recursive decision-making usually, is likely one of the strongest candidates towards this holy grail (by the way in which, I feel the opposite robust contenders are (1) model-based RL and (2) TD studying with some “magic” methods). Certainly, a number of current works in different fields have proven the promise of recursion and divide-and-conquer methods, equivalent to shortcut fashions, log-linear consideration, and recursive language fashions (and naturally, basic algorithms like quicksort, phase bushes, FFT, and so forth). I hope to see extra thrilling progress in scalable off-policy RL within the close to future!
Acknowledgments
I’d wish to thank Kevin and Sergey for his or her useful suggestions on this put up.
This put up initially appeared on Seohong Park’s weblog.

